Note 13. Spatial Theory
The Geometry of Legislating
When we speak of most Democrats as liberals and on the left, most Republicans as conservatives and on the right, and some legislators as moderates and in the middle, we have in mind a geometric representation of policy or ideological views. We think of legislators as distributed across a line or dimension. In recent Congresses, the parties have been sharply divided with very little overlap between the parties on the liberal-conservative dimension (see Note 1).
Legislators’ policy positions also can be represented in two or more dimensions, when appropriate. In 2021, for example, the Senate considered a bill to expand federal programs that support science and technology research and innovation, to support American manufacturing of microchip and communications products, and to put in place penalties and other efforts to combat unfair technological practices of China. The bill included federal spending for research and development that conservative often oppose and liberals often support, but it also had provisions to address the economic and national security challenges posed by China. These represented different dimensions—legislators who differ on provisions concerning American electronics industry development may agree on American responses to a Chinese threat to national security. In the end, that’s what happened—68 senators, 49 Democrats and 19 Republicans—voted in favor to the bill. Against the bill were 31 Republicans and one Democrat. The Democrat, Bernie Sanders (I-VT), opposed giving federal funding directly to large American companies that produce digital products.
Political scientists have taken advantage of geometric representations to develop spatial theories of legislative politics. Spatial theories assume the legislators, presidents, and other players have preferences about policy outcomes. Preferences may reflect personal beliefs or political influences. The preferences are assumed to be consistent. For example, if a legislator prefers policy A over policy B and also prefers B over C, then she favors A over C (transitive preferences). When a legislator’s preference is depicted geometrically, as in the figures below, it is assumed that alternatives that are closer to the legislator’s ideal point are preferred to more distant points (a Euclidean policy space). Furthermore, it is assumed that each legislator chooses a strategy that she believes will yield the best possible outcome – that is, minimizes the distance between her ideal point and the outcome.
Simple Majority Rule and the Median Voter Theorem
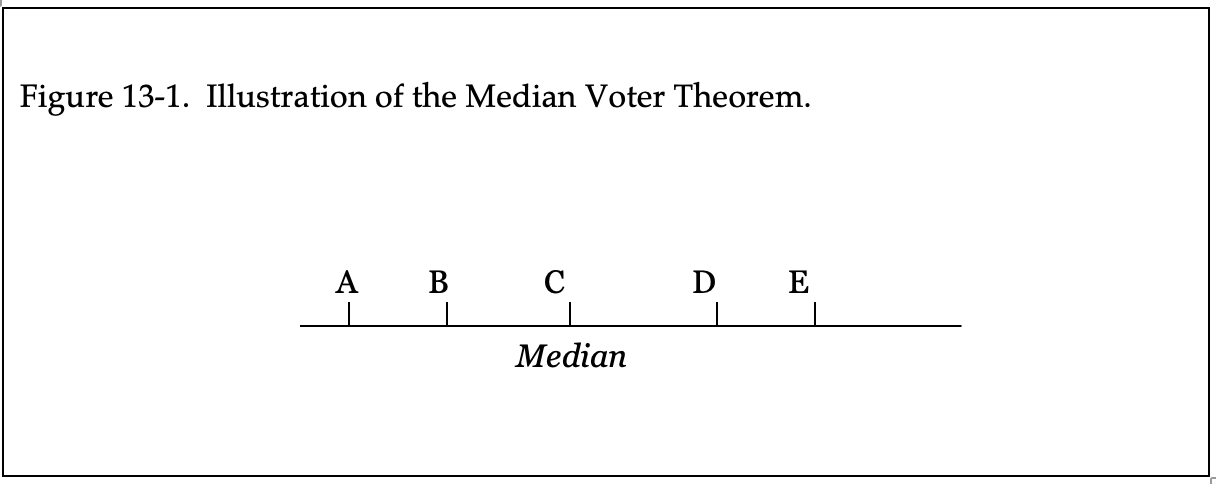
Let’s assume that each legislator has the right to cast one vote and, to begin, that a simple majority of legislators is required for a proposal to be adopted. In Figure 13-1, a small legislature with five legislators is illustrated. With a simple majority decision rule, a winning majority will always include legislator C. As the median legislator, C can join two other legislators – to the left with A and B, to the right with D and E, or in the middle with B and D – to form a three-vote majority. Of course, larger majorities could form, but they will always include C. A spatial theorist would say that C is pivotal–C must be included in a majority and so can demand that the outcome be located at her ideal point. The median voter theorem, which we will not formally prove here, provides that if C’s position is adopted it cannot be defeated by another proposal. A corollary is that if two alternatives are presented, a majority will always prefer the alternative closer to the median legislator.
The median voter theorem means that when a median exists we can predict the outcome by knowing only the median legislator’s ideal point. Spatial theorists refer to the prediction of the median outcome as an equilibrium—a stable outcome. When a new legislature is elected, a new median location would lead us to predict a change in the outcome. That is, a new equilibrium is expected.
Multidimensional Spaces and the Chaos Theorem
A multidimensional policy space creates important complications for predicting legislative outcomes. Let’s imagine one. One complicated issue is American immigration policy. In practice, there are many dimensions to immigration policy, but let’s focus on a hypothetical bill that addresses two of them—whether or not to grant amnesty to people who already have entered the U.S. illegally and whether the number of people allowed to immigrate legally (quotas) should be increased or decreased.
In Figure 13-2, the five legislators are arrayed on the amnesty issue (the horizontal dimension) just as they were in Figure 13-1 (A-B-C-D-E). The quota dimension arrays the legislators in a different order (A-D-E-B-C).
Notice that no legislator is the median on both dimensions. C is the median on the amnesty dimension but E is the median on the quota liberalization dimension. What is the expected outcome? Political scientists have demonstrated mathematically that in most cases there is no single predicted outcome, no equilibrium, when there are two or more dimensions. A median is guaranteed only in the unidimensional case.
A thought experiment will demonstrate an important point. Let us assume that current policy is located at x1 in Figure 13-2. Legislator B might propose a policy at x2 and would win the support of A and C, both of whom are closer to x1 than to x2 and so would join B to form a majority to vote for x2 and defeat x1.
But then D might offer x3 and win the support of A and E. This process can continue indefinitely with a new majority of three forming at each step. If the rules allow a continuous flow of new proposals, there is no single outcome that cannot be defeated by some other proposal. This illustrates the chaos theorem. The theorem provides that, as a general rule when proposals may be considered in such a sequence, we cannot expect a stable outcome from simple majority rule in two (or more) dimensions.
Agenda Setting, Structure-Induced Equilibria, and Political Power
The chaos result – or majority rule cycling – may seem surprising. Legislatures regularly make final decisions without endless cycling through proposals. Why that is the case is the subject of a vast literature in political science. We do not want to review the complexities here, but three important points about legislative politics need to be understood.
1. Legislative rules may not allow multidimensional proposals or may limit the number of proposals that may be considered. Such rules would limit the range of possible outcomes and make outcomes more predictable. The median voter theorem applies only when the space is unidimensional.
Theorists use the label structure-induced equilibria for constraints on outcomes that are imposed by the rules. Thus, even if legislators’ preferences are multidimensional, the rules may generate median outcomes by either limiting the range of proposals that are allowed or imposing unidimensionality on the proposals that may be considered.
2. Special influence over the agenda, either granted under the rules or gained through informal means, may control the alternatives subject to a vote and further limit the possible outcomes. A Speaker or presiding officer may be able to limit who is recognized to offer a motion. A coalition of legislators, such as members of the majority party, may agree to support only those proposals that a majority of the coalition endorses, thus limiting the set of proposals that can win majority support.
3. Introducing a proposal that creates a new dimension can transform a situation that would produce a median outcome into one with no predictable outcome. A legislator who dislikes the median outcome might be motivated to offer a proposal on an issue that divides his colleagues in a new way in order to avoid the certain, but undesirable outcome. The original median legislator would be motivated to create an agenda that prevents the proposal on the new issue from being considered.
In practice, then, rules and legislative strategies can contract or expand the range of possible outcomes. Real politics is often played in this way.
The Status Quo and Agenda Setting
A legislature often inherits policy from past legislatures. In most cases, the inherited policy, which we call the status quo (SQ), remains in place until a new policy is adopted. That is, the SQ is the default outcome if it is not defeated by a new proposal. The set of proposals that can defeat the SQ is called the win set of SQ. When there are no proposals that can defeat the SQ, we say that the win set is empty and predict that the outcome will remain at SQ.
The effect of the SQ on legislative strategies is important and intuitive. In Figure 13-3, five legislators are arrayed on a single dimension. In the figure’s top panel, let’s assume that no proposal can be considered unless legislator E approves, but if a proposal is offered it can be amended. E, of course, wants the outcome at her own ideal point and might make a proposal there. However, A, B, or C might offer an amendment to move the outcome away from E and to the other side of SQ. Such an amendment would win a majority and E would be worse off than if he left the policy at SQ. Consequently, we would expect E to refuse to make an initial proposal. In this case, the agenda setter, E, protects the status quo.
In contrast, in the lower panel of Figure 13-3, legislator A is the agenda setter. Because A prefers the median’s position over the SQ, A is willing to allow the legislature to consider a proposal and have it amended to C, the expected outcome.
Thus, the location of the status quo relative to the median determines the agenda setter’s strategy. With the same agenda setter and median, different issues can generate different outcomes– the median or the SQ.
The same logic applies to the multidimensional case, as in Figure 13-4. Legislators will support a proposal that improves on the status quo, SQ. In the figure, these preferred-to sets are denoted by the partial or full circles. For example, within the shaded circle centered on legislator A is the preferred-to set for A. The double shaded areas are the sets of locations preferred by at least three of the five legislators over SQ. Because points in the double shaded areas attract majority support for a proposal over the SQ, they define the win set of SQ. A large number of locations will not defeat SQ so majority rule narrowed the possible outcomes considerably. But, in this two-dimensional space, the win set includes a wide range of possibilities, many of which are less preferred to the SQ by one or two of the legislators. A, B, and D might agree to an outcome at x, which would make C and E worse off than leaving the policy at SQ.
Bicameralism
So far we have considered a single legislative body. Congress is bicameral and, for most issues, a majority of each chamber is required to approve legislation before it is sent to the president. Spatially, this means that we must consider the relationship between the outcomes in the two chambers.
In unidimensional space, shown Figure 13-5, the outcome would be negotiated between the House and Senate medians. If both medians favor some of the same proposals over SQ, as they do in the top panel, they will negotiate an outcome in the range of proposals that they both prefer to SQ. If SQ falls between the two medians so that each house median prefers SQ to anything the other house would prefer to SQ, as in the figure’s lower panel, the houses will not agree to a new policy and the outcome will be SQ.
In multidimensional space—say, something like Figure 13-4—we would define the bicameral win set as the intersection of the win sets in the two houses. We do not show that situation here. The overlap in the win sets for the two houses can be very small or very large. Little overlap greatly narrows the range of possible outcomes. Large overlap creates the possibility that a conference committee charged with finding compromise legislation will be able to exercise great discretion in determining the location of the final bill and still be able to attract majority support in both houses for the final version.
The President and the Veto
Under the Constitution, the president may veto legislation and a veto can be overridden only with the support of a two-thirds majority in each house of Congress. The threshold of a two-thirds majority in each house makes it necessary to appeal to more legislators than the requirement of a simple majority for initial approval of legislation. In our five-legislators illustrations, this means attracting the support of four of the five legislators (three of five would be less than the two-thirds required).
The president will veto any legislation that makes him worse off than SQ. In one dimension, several possibilities arise. In Figure 13-6 the president’s ideal point is P and the House and Senate medians are MH and MS, respectively. The two houses of Congress negotiate a bill at B somewhere between their medians. The president prefers SQ to B so he vetoes the bill. Both House and Senate medians would like to override the veto but they must gain the support of two-thirds of their colleagues. VH and VS are the veto pivots. That is, they are the legislators who are the leftmost members of the two-thirds majority that is required to override a veto. Without their support for the bill over the SQ, the veto cannot be overridden. In this case, VH prefers SQ to Band so votes against the override. SQ is the outcome. Thus, the general rule is that a presidential veto will kill a bill whenever at least one of the veto pivots is on the same side of SQ as the president.
Other scenarios are easy to understand without illustration. Whenever the chamber medians are on the same side of SQ as the president, the president will sign the bill with a veto. Whenever VH and VS are on the same side of SQ opposite the president (not shown), the two houses of Congress can override the veto of the president.
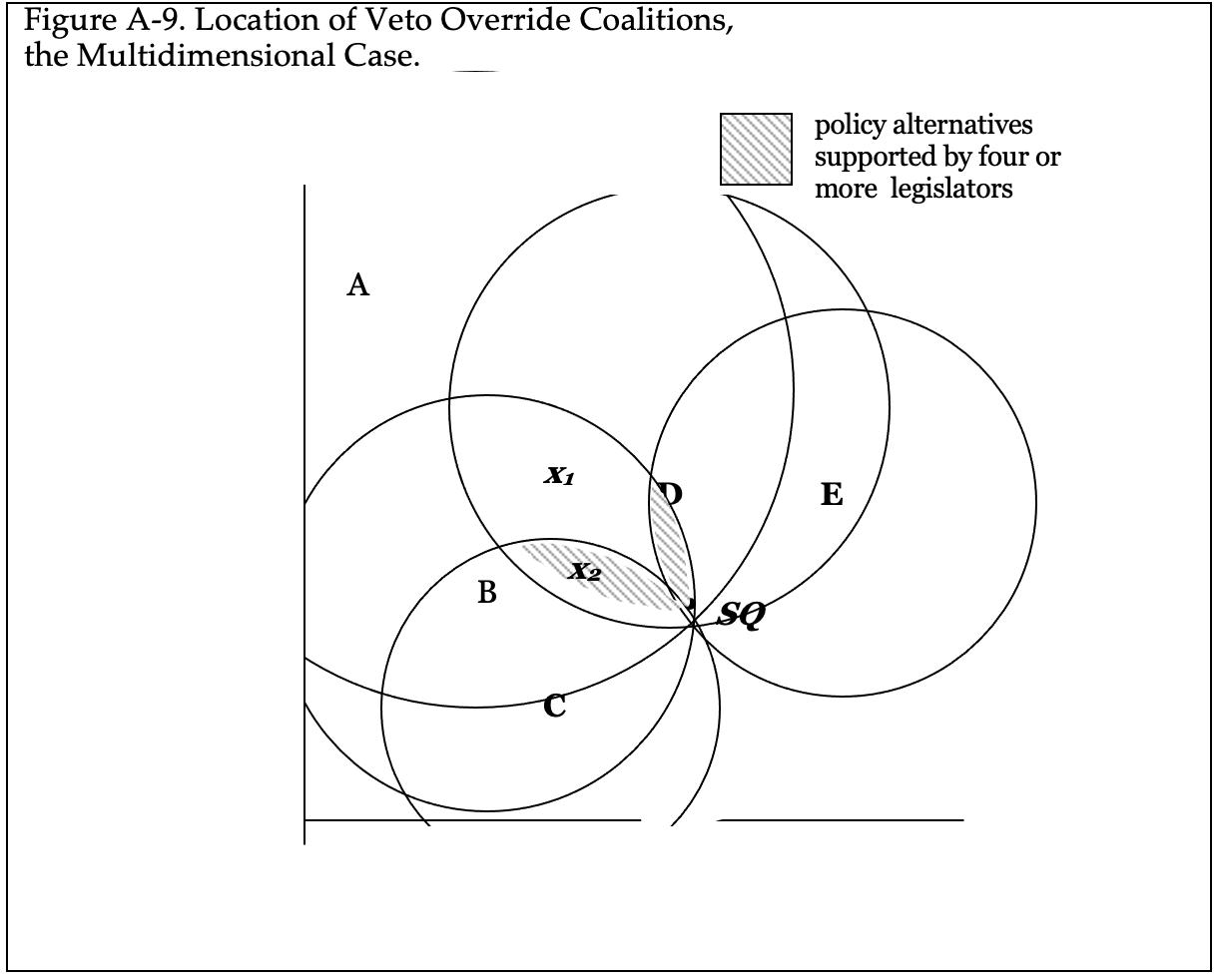
As always, the multidimensional case is more complicated but it is still easy to visualize. In Figure 13-7, there are two regions in which four of the five legislators of one house would favor the bill over the SQ. Consequently, a veto would be overridden any time the president vetoes a bill that is located in those regions. The bill also would have to be located in similar regions in the other house for both houses to override a president’s veto. A bill that is located in the veto win set ofSQ is one for which a veto can be overridden in both houses.
Plainly, the two-thirds majority requirement for a veto override shrinks the region of bill locations that can survive a veto to one that is smaller than the region of bill locations that can receive simple majority support in both houses. The implication is that the threat of a veto requires more careful negotiations within Congress and may have implications for legislators who win and lose. In Figure 13-7, for example, the bill at x2survives a veto but a bill at x1 does not, although both would receive simple majority support. But the outcome at x2 is less favorable to legislators A and D and more favorable to B and C.
Agency Decisions
Political scientists often think of executive branch agencies as having policy preferences of their own. Staffed by people who have personal or professional experience in a policy field, agencies are likely to devise rules and regulations that implement law in a manner that reflects their own preferences. Congress and presidents may seek to control the independence of agencies, but agency officials know that it may not be easy for Congress and the president to enact new legislation to place additional constraints on them. After all, new legislation requires the approval of the House, Senate, and president, or, in the case of a veto, a two-thirds majority in both houses. This is a high threshold. If a House majority, Senate majority, or president favors the direction an agency is taking, it can block legislation that would place new constraints in statute.
The strategic setting of agency decision making can be treated spatially, as we do in Figure 13-8. To simplify, we characterize the House and Senate as having specific locations in multidimensional space just as the president does. If an agency took action to move a policy from a1 (the current policy) to a2, the Senate would like the move and block any effort by the House to enact legislation to require that the policy be returned to a1. In this case,the agency, knowing that the Senate will protect its move, is free to shift policy without fear that the law will be changed. In contrast, if the agency sought to move policy as far as a3, all three of the policy-making institutions would be better off by enacting legislation located on the line between S and P.
These scenarios demonstrate that the autonomy of an agency is limited to the range of policy moves that will not generate a new law. The farther apart the House, Senate, and president, the greater the discretion the agency enjoys. In fact, the triangle formed by the House, Senate, and president defines the limits of agency discretion. Any move that yields policy inside or to the edge of the triangle will be defended by at least one of the House, Senate, or president. Any move outside of the triangle will stimulate new legislation.
Nevertheless, spatial theory is a powerful tool for predicting behavior and legislative outcomes. It often establishes a baseline expectation for outcomes against which the effects of other considerations can be measured. We can better judge the effects of persuasion by party leaders or presidents once we have a prediction for the outcome expected on the basis of legislators’ prior policy preferences. It also shows that policy preferences and parliamentary rules often do not yield very specific predictions and define sometimes large ranges of possible outcomes that can be influenced by other political forces at work. Most important, spatial theory yields important insights about the effects of institutions – the rules of the game – that are so transparent in legislative decision making.
The Limits of Spatial Theory
Spatial theory is not the ultimate theory of legislative politics. The spatial theorist assumes that legislators’ policy preferences are known and invariant and theorizes only about how they motivate strategies. The determinants of legislators’ policy preferences are beyond the scope of spatial theory.
The effects of nonpolicy motivations, such as the desire for reelection or to serve in the majority party, also are beyond the scope of spatial theory. Such motivations may be the overriding consideration in some circumstances. A legislator whose bill is rejected by the House of Representatives might be seen as a loser by some observers, but she may benefit from favorable press coverage and an appreciative home constituency for putting up a good fight. A legislative majority that fails to override a presidential veto may use the issue in a campaign to get more fellow partisans elected in the next Congress. Winning and losing in politics is sometimes hard to judge, at least in the short term.